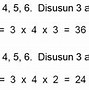
Suatu saat Ani akan pergi ke taman bermain bersama teman-temannya. Namun, dia bingung memilih baju dan celana yang akan di pakai. Dia memiliki dua baju yang berwarna abu-abu dan warna merah. Sedangkan celananya ada tiga jenis yaitu celana warna biru, pink dan hijau. Pertama, Ani mencoba pasangan baju abu-abu dan celana hijau. Namun, kemudian dia mencoba lagi pasangan yang lain. Ani kemudian ingin mencoba semua pasangan baju yang mungkin dia pakai. Tahukah kalian sebenarnya berapa banyak pasanng baju dan celana yang mungkin dipakai oleh Ani?
Untuk menyelesaikan masalah diatas sebenarnya bisa pula dengan menghitung manual yaitu dengan metode diagram pohon atau metode tabel. Berikut ini contoh menghitung pasangan baju yang mungkin dipakai dengan kedua metode tersebut:
Metode manual di atas cukup efektif untuk digunakan tetapi tidak efisien jika banyak baju dan celana sangatlah banyak atau mungkin ditambah kombinasi dari sepatu misalnya. Kalian harus menggambar atau menulis satu-persatu sampai semua pasang yang mungkin dapat dihitung. Oleh karena itu, munculah metode filling slots atau metode pengisian tempat.
Perhatikan dan baca kembali masalah Ani di atas. Ani akan memilih satu baju dan satu celana untuk dipakai dari 2 baju dan 3 celana berbeda yang dia miliki. Artinya Ada dua tempat yang perlu diisi yaitu slot untuk baju dan slot untuk celana.
Pada slot pilihan baju, Ani memiliki 2 pilihan baju yaitu warna abu-abu dan merah. Oleh karena itu, slot baju ditulis 2 karena Ani punya 2 pilihan baju. Sedangkan untuk slot pilihan celana, Ani memiliki 3 celana berbeda yaitu biru, pink, dan hijau. Oleh karena itu, slot celana ditulis 3 karena Ani memiliki 3 pilihan celana. Banyaknya pasangan yang mungkin diperoleh dengan cara mengalikan pilihan yang ada pada slots.
Jadi Ani memiliki 6 pasang baju dan celana yang mungkin dipakai.
Berdasarkan contoh di atas, secara umum Metode Pengisian Tempat (Filling Slots) yaitu sebagai berikut:
Jika terdapat n buah tepat tersedia dengan:
k1 adalah banyak cara atau pilihan untuk mengisi tempat pertama,
k2 adalah banyak cara atau pilihan untuk mengisi tempat kedua, setelah tempat-tempat sebelumnya terisi.
k3 adalah banyak cara atau pilihan untuk mengisi tempat ketiga, setelah tempat-tempat
kn adalah banyak cara atau pilihan untuk mengisi tempat ke-n, setelah tempat-tempat
Maka banyak cara mengisi n tempat yang tersedia secara keseluruhan adalah
k1 x k2 x k3 x … x kn
Untuk lebih memahami metode pengisian tempat. Lihat dan pahamilah contoh berikut:
Diketahui angka-angka 2, 3, 4, 5, 6, 7, dan 8. Carilah banyak cara memilih tiga angka dari angka-angka tersebut agar:
Ada tiga tempat yang harus diisi yaitu
Assalamualaikum wr. Wb
Kamis…. memulai pagi ini dengan senyuman manis penuh optimis. Ucapan doa dan syukur, semoga apapun yang kita kerjakan khususnya sekarang dalam Pembelajaran Jarak Jauh, semoga selalu mendapatkan kemudahan dari Allah. Ilmu yang di pelajari semoga memberi manfaat untuk kehidupan kalian.
Sebelumnya ibu akan menanyakan materi yang sudah dipelajari apakah kalian sudah mengerti atau belum? Mudah-mudahan kalian bisa memahaminya ya….
Naah sekarang yang akan di pelajari adalah counting slots (kaidah pencacahan), yang mana tujuan dari pembelajaran adalah sebagai berikut :
Apabila kejadian pertama dapat diselesaikan dengan n1 cara, diikuti kejadian kedua dengan n2 cara, diikuti kejadian dengan n3 cara… dan seterusnya, maka keseluruhan kejadian dalam urutan demikian dapat diselesaikan dengan n1 + n2 + n3 +… cara.
Aturan penjumlahan biasanya digunakan untuk beberapa kejadian yang tidak sekaligus terjadi, artinya yang terjadi hanya satu kali saja atau bisa dibilang pilihan dan biasanya menggunakan kata penghubung “ATAU”
Atuaran penjumlahan digunakan jika :
Pengertian Kaidah Pencacahan (Counting Slots)
Kaidah pencacahan atau Caunting Slots adalah suatu kaidah yang digunakan untuk menentukan atau menghitung berapa banyak cara yang terjadi dari suatu peristiwa. Kaidah pencacahan terdiri atas :
1). Pengisian Tempat yang Tersedia (Filling Slots)
Apabila suatu peristiwa pertama dapat dikerjakan dengan k1 cara yang berbeda, peristiwa kedua dapat dikerjakan dengan k2 yang berbeda dan seterusnya sampai peristiwa ke-n, maka banyaknya cara yang berbeda dari semua peristiwa tersebut adalah K, di mana :
Untuk menentukan banyaknya tempat yang tersedia selain menggunakan aturan perkalian, juga menggunakan diagram pohon, tabel silang, dan pasangan berurutan
Naaah untuk lebih jelasnya mengenai materi yang akan kalian pelajari coba buka slide berikut ook…
Dari kota x menuju kota y terdapat beberapa jenis angkutan yang dapat digunakan. Ada 5 bus, 2 kapal laut, 3 pesawat terbang, dan 4 kereta api. Banyak cara berbeda untuk berangkat dari kota x menuju kota y menggunakan jenis angkutan tersebut adalah ….